Graph

그래프의 특징

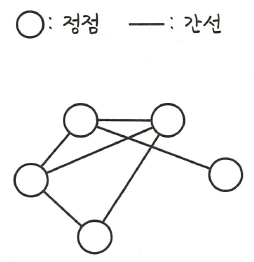
그래프(graph)는 정점(vertex = 노드(node))와 간선(edge)로 구성된 자료구조이다.

그래프는 간선이 정점들을 잇는 형태로 구성된다.

 

그래프의 종류

그래프는 간선의 형태에 따라 무향 그래프(undirected graph)와 방향 그래프(directed graph)로 구분된다.

 

무향 그래프

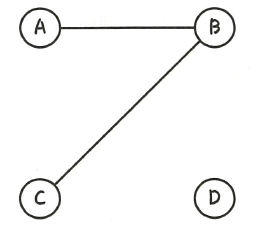
무향 그래프는 간선에 방향이 없는 그래프를 의미한다. 

무향 그래프에서 간선으로 이어진 정점은 방향에 상관없이 서로에게 이동할 수 있다.

 

방향 그래프

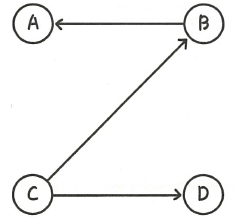
방향 그래프는 간선에 방향이 있는 그래프를 의미한다.

방향 그래프에서 간선으로 이어진 정점은 간선의 방향대로만 이동할 수 있다.

 

그래프의 구현 방법

그래프를 구현할 수 있는 대표적인 방법으로는 인접 행렬(adjacency matrix)과 인접 리스트(adjacency list)가 있다.

 

인접 행렬

인접 행렬은 그래프를 정사각형 모양의 2차원 배열로 구현하는 방법이다.

2차원 배열의 각 인덱스는 정점을 의미한다.

원소는 정점 사이에 이동할 수 있는 간선이 있는지 여부를 나타낸다. 더 정확히 말하자면 외부 배열의 정점에서 내부 배열의 정점으로 이동할 수 있는 간선이 있는지 여부를 나타낸다.

 

무향 그래프의 인접 행렬

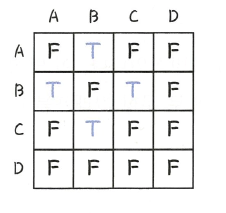
위의 그림은 글 상단에서 봤던 무향 그래프를 인접 행렬로 나타낸 그림이다.

양쪽으로 이동 가능한 무향 그래프이기 때문에 graph[0][1]과 graph[1][0]이 모두 true인 것을 볼 수 있다.

 

방향 그래프의 인접 행렬

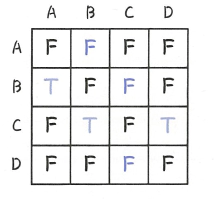
위의 그림은 글 상단에서 봤던 방향 그래프를 인접 행렬로 나타낸 그림이다.

간선의 방향대로만 이동 가능한 방향 그래프이기 때문에 graph[1][0]은 true이지만 graph[0][1]은 false이다.

 

인접 리스트

인접 리스트는 리스트를 원소로 가지는 1차원 배열 또는 리스트로 그래프를 구현하는 방법이다.

1차원 배열 또는 리스트의 인덱스는 정점을 나타낸다.

그리고 각 인덱스에 담긴 리스트는 해당 인덱스가 의미하는 정점의 인접 정점들에 대한 정보를 담는다.

 

무향 그래프의 인접 리스트

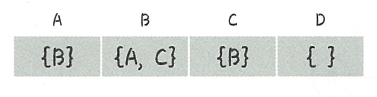
위의 그림은 글 상단에서 봤던 무향 그래프를 인접 리스트로 나타낸 그림이다.

 

방향 그래프의 인접 리스트

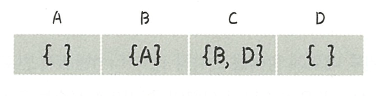
위의 그림은 글 상단에서 봤던 방향 그래프를 인접 리스트로 나타낸 그림이다.

 

그래프의 구현

인접 행렬을 통한 그래프 구현

AdjMatrix

public class AdjMatrix {

	private int[][] adjMatrix;

	public AdjMatrix(int size) {
		adjMatrix = new int[size + 1][size + 1]; // vertex의 인덱스를 1부터 시작하기 위함.
	}

	// 무향 간선 - 가중치 X
	public void insertBiDir(int vertex1, int vertex2) {
		adjMatrix[vertex1][vertex2] = 1;
		adjMatrix[vertex2][vertex1] = 1;
	}

	// 무향 간선 - 가중치 O
	public void insertBiDir(int vertex1, int vertex2, int weight) {
		adjMatrix[vertex1][vertex2] = weight;
		adjMatrix[vertex2][vertex1] = weight;
	}

	// 방향 간선 - 가중치 X
	public void insertSingleDir(int vertex1, int vertex2) {
		adjMatrix[vertex1][vertex2] = 1;
	}

	// 방향 간선 - 가중치 O
	public void insertSingleDir(int vertex1, int vertex2, int weight) {
		adjMatrix[vertex1][vertex2] = weight;
	}

	@Override
	public String toString() {
		StringBuilder sb = new StringBuilder();

		for (int i = 1; i < adjMatrix.length; i++) {
			for (int j = 1; j < adjMatrix[i].length; j++) {
				sb.append(adjMatrix[i][j]).append(" ");
			}
			sb.append("\n");
		}

		return sb.toString();
	}
}

 

실제 사용

public class Main {

	public static void main(String[] args) {
		AdjMatrix adjMatrix = new AdjMatrix(5);

		adjMatrix.insertSingleDir(1, 3, 2);
		adjMatrix.insertSingleDir(3, 2, 3);
		adjMatrix.insertBiDir(4, 5, 4);

		System.out.print(adjMatrix.toString());
		/*0 0 2 0 0
		  0 0 0 0 0
		  0 3 0 0 0
		  0 0 0 0 4
		  0 0 0 4 0*/
	}
}

 

인접 리스트를 통한 그래프 구현

Edge

public class Edge {
	private int destination;
	private int weight;

	public Edge(int destination, int weight) {
		this.destination = destination;
		this.weight = weight;
	}

	public Edge(int destination) {
		this.destination = destination;
		this.weight = 1;
	}

	public int getDestination() {
		return destination;
	}

	public int getWeight() {
		return weight;
	}
}

 

AdjList

public class AdjList<T> {
	private int size; // 정점들의 개수
	private List<List<Edge>> adjList = new ArrayList<>(); // 정점들의 목록
	private List<T> dataList = new ArrayList<>(); // 정점들의 데이터를 저장한다.

	// 정점 추가
	public void addVertex(T data) {
		adjList.add(new ArrayList<>()); // 정점들의 목록을 추가한다.
		dataList.add(data); // 정점들의 데이터를 저장한다. 동일한 정점에 대한 adjList와 dataList의 인덱스는 동일하다.
		size++; // 정점 개수 증가
	}

	// 간선을 추가한다 - 가중치 지정
	public void addEdge(int source, int destination, int weight) {
		adjList.get(source).add(new Edge(destination, weight));
	}

	// 간선을 추가한다 - 가중치 지정
	public void addEdge(int source, int destination) {
		adjList.get(source).add(new Edge(destination));
	}

	// 주어진 인덱스에 해당하는 정점의 인접 정점을 반환한다.
	public List<Edge> getAdjVertices(int index) {
		return adjList.get(index);
	}

	// 주어진 인덱스에 해당하는 정점의 데이터를 반환한다.
	public T getData(int index) {
		return dataList.get(index);
	}

	@Override
	public String toString() {
		StringBuilder sb = new StringBuilder();

		for (int i = 0; i < adjList.size(); i++) {
			sb.append("adjVertices to " + i + ": ");
			List<Edge> adjVertices = getAdjVertices(i);

			for (Edge adjVertex : adjVertices) {
				sb.append(adjVertex.getDestination() + "(" + adjVertex.getWeight() + ")" + " ");
			}

			sb.append("\n");
		}

		return sb.toString();
	}
}

 

실제 사용

public class Main {

	public static void main(String[] args) {
		AdjList<Integer> graph = new AdjList<>();

		for (int i = 1; i <= 5; i++) {
			graph.addVertex(i);
		}

		graph.addEdge(0, 2, 2);
		graph.addEdge(0, 3, 4);
		graph.addEdge(1, 4);
		graph.addEdge(3, 4, 6);

		System.out.print(graph.toString());
		/*adjVertices to 0: 2(2) 3(4)
		  adjVertices to 1: 4(1)
		  adjVertices to 2:
		  adjVertices to 3: 4(6)
		  adjVertices to 4:*/
	}
}